Pictures and movies of random lozenge tilings
2016/08/20
In Spring 2015 and Summer 2016 I used the Python and Mathematica
as
briefly
described here
to produce a number of pictures and “movies” of random lozenge tilings.
Some of these pictures even appeared at an art exhibition at Harvard’s Radcliffe Institute accompanying Alexei Borodin’s fellowship.
These pictures and “movies” of random tilings are collected in this post.
Dear colleagues:
Feel free to use these pictures to illustrate your research in talks and papers, with attribution (CC BY-SA 4.0). Some of the images are available in very high resolution upon request.
Links to images
[1] • 1.5 MB •
Uniformly random tiling of a 9-gon
[2] • 1.5 MB •
Uniformly random tiling of another 9-gon
[3] • 1.5 MB •
Uniformly random tiling of a hexagon of height 120
[4] • 1.5 MB •
Uniformly random tiling of a 12-gon
[5] • 6 MB •
Growth of a tiling of a 9-gon
[6] • 11 MB •
Growth of a tiling of a 12-gon of height 200 (only vertical tiles are shown)
[7] • 1.5 MB •
Result of the previous simulation
[8] • 11 MB •
Growth of a tiling of a 12-gon of height 200 (only vertical tiles are shown). Slower simulation, does not reach equilibrium yet
[9] • 12 MB •
Growth of a tiling of a 12-gon of height 200 (only vertical tiles are shown). Faster simulation, seems to reach the equilibrium
[10] • 19 MB •
Growth of a random q-weighted tiling of a hexagon of height 100, part 1. Reaching the equilibrium
[11] • 20 MB •
Growth of a random q-weighted tiling of a hexagon of height 100, part 2. Equilibrium dynamics
[12] • 1 MB •
Result of the previous two simulations, q-weighted random tiling of a hexagon of height 100
[13] • 11 MB •
Growth of a random q-weighted tiling of a 12-gon, part 1
[14] • 11 MB •
Growth of a random q-weighted tiling of a 12-gon, part 2
[15] • 13 MB •
Growth of a random q-weighted tiling of a 12-gon, part 3
[16] • 1 MB •
Result of the previous three simulations
[17] • 6 MB •
Growth of a uniformly random tiling of a 27-gon of height 200, part 1. The starting configuration is not interlacing (easier to code), but the interlacing configurations form an absorbing class for the Glauber Markov chain. Note the two outliers on the right
[18] • 14 MB •
Growth of a uniformly random tiling of a 27-gon of height 200, part 2
[19] • 18 MB •
Growth of a uniformly random tiling of a 27-gon of height 200, part 3
[20] • 20 MB •
Growth of a uniformly random tiling of a 27-gon of height 200, part 4
[21] • 22 MB •
Growth of a uniformly random tiling of a 27-gon of height 200, part 5
[22] • 2 MB •
Result of the above five simulations
[23] • 1 MB •
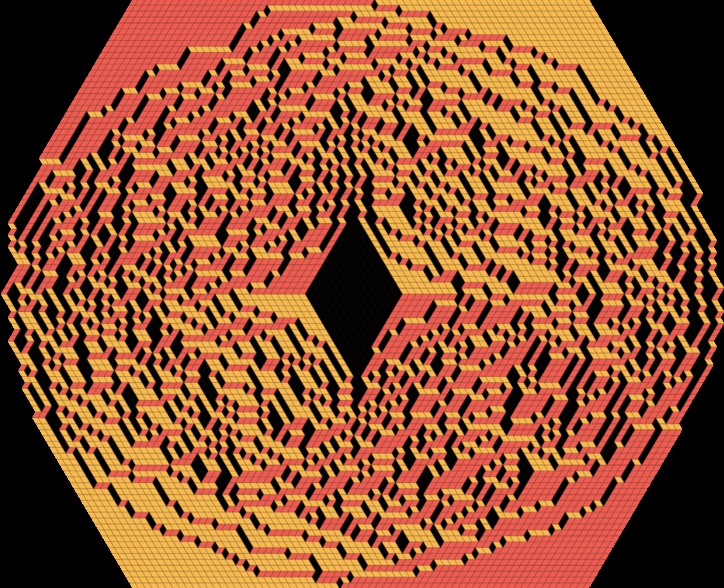
Sauron's eye - a tiling of a hexagon with a hole
[24] • 1 MB •
Sauron's eye on a fully black background
[25] • 1 MB •
Skewed Sauron's eye
[26] • 2 MB •
Tiling of a ghost (a polygon with 2 holes)
[27] • 2 MB •
Random heart in UVA colors
[28] • 1 MB •
Random heart, yet another color version (red-green-white)
[29] • 1 MB •
Random heart, yet another color version (blue-red)
[30] • 1 MB •
Random heart, yet another color version (dark red)
[31] • 1 MB •
Random heart, yet another color version (red-yellow-light green)
[32] • 1 MB •
Random heart, yet another color version (red-yellow-black)
[33] • 1 MB •
Random heart, yet another color version (red-yellow-light blue)
[34] • 300 KB •
Random ghost, dot variant 1
[35] • 1 MB •
Random ghost, dot variant 2
[36] • 1 MB •
Random ghost, color version 1
[37] • 600 KB •
Random ghost, color version 2
[38] • 600 KB •
Random ghost, color version 3
Sauron's eye
