Preprints

  1. Greta Panova, Leonid Petrov. Hook-length Formulas for Skew Shapes via Contour Integrals and Vertex Models (2024) • arXiv:2409.17842 [math.CO] • (PDF)
    Abstract

    The number of standard Young tableaux of a skew shape $\lambda/\mu$ can be computed as a sum over excited diagrams inside $\lambda$. Excited diagrams are in bijection with certain lozenge tilings, with flagged semistandard tableaux and also nonintersecting lattice paths inside $\lambda$. We give two new proofs of a multivariate generalization of this formula, which allow us to extend the setup beyond standard Young tableaux and the underlying Schur symmetric polynomials. The first proof uses multiple contour integrals. The second one interprets excited diagrams as configurations of a six-vertex model at a free fermion point, and derives the formula for the number of standard Young tableaux of a skew shape from the Yang-Baxter equation.

    Yang-Baxter equation meets Young diagrams
  2. Alejandro H. Morales, Greta Panova, Leonid Petrov, Damir Yeliussizov. Grothendieck Shenanigans: Permutons from pipe dreams via integrable probability (2024) • arXiv:2407.21653 [math.PR] • (PDF)
    Abstract

    We study random permutations arising from reduced pipe dreams. Our main model is motivated by Grothendieck polynomials with parameter $\beta=1$ arising in K-theory of the flag variety. The probability weight of a permutation is proportional to the principal specialization (setting all variables to 1) of the corresponding Grothendieck polynomial. By mapping this random permutation to a version of TASEP (Totally Asymmetric Simple Exclusion Process), we describe the limiting permuton and fluctuations around it as the order $n$ of the permutation grows to infinity. The fluctuations are of order $n^{\frac{1}{3}}$ and have the Tracy-Widom GUE distribution, which places this algebraic (K-theoretic) model into the Kardar-Parisi-Zhang universality class.

    We also investigate non-reduced pipe dreams and make progress on a recent open problem on the asymptotic number of inversions of the resulting permutation. Inspired by Stanley’s question for the maximal value of principal specializations of Schubert polynomials, we resolve the analogous question for $\beta=1$ Grothendieck polynomials, and provide bounds for general $\beta$.

    Reduction of a pipe dream leading to the permutation w(D) = 241653.
  3. Amol Aggarwal, Matthew Nicoletti, Leonid Petrov. Colored Interacting Particle Systems on the Ring: Stationary Measures from Yang--Baxter Equation (2023) • arXiv:2309.11865 [math.PR] • (PDF) • (TeX)
    Abstract

    Recently, there has been much progress in understanding stationary measures for colored (also called multi-species or multi-type) interacting particle systems, motivated by asymptotic phenomena and rich underlying algebraic and combinatorial structures (such as nonsymmetric Macdonald polynomials).

    In this paper, we present a unified approach to constructing stationary measures for most of the known colored particle systems on the ring and the line, including (1) the Asymmetric Simple Exclusion Process (multispecies ASEP, or mASEP); (2) the q-deformed Totally Asymmetric Zero Range Process (TAZRP) also known as the q-Boson particle system; (3) the q-deformed Pushing Totally Asymmetric Simple Exclusion Process (q-PushTASEP). Our method is based on integrable stochastic vertex models and the Yang-Baxter equation. We express the stationary measures as partition functions of new “queue vertex models” on the cylinder. The stationarity property is a direct consequence of the Yang-Baxter equation.

    For the mASEP on the ring, a particular case of our vertex model is equivalent to the multiline queues of Martin. For the colored q-Boson process and the q-PushTASEP on the ring, we recover and generalize known stationary measures constructed using multiline queues or other methods by Ayyer-Mandelshtam-Martin (1, 2, and Bukh-Cox. Our proofs of stationarity use the Yang-Baxter equation and bypass the Matrix Product Ansatz (used for the mASEP by Prolhac-Evans-Mallick).

    On the line and in a quadrant, we use the Yang-Baxter equation to establish a general colored Burke’s theorem, which implies that suitable specializations of our queue vertex models produce stationary measures for particle systems on the line. We also compute the colored particle currents in stationarity.

    Yang-Baxter equation implies colored Burke theorem

Published or accepted • (Full CV)

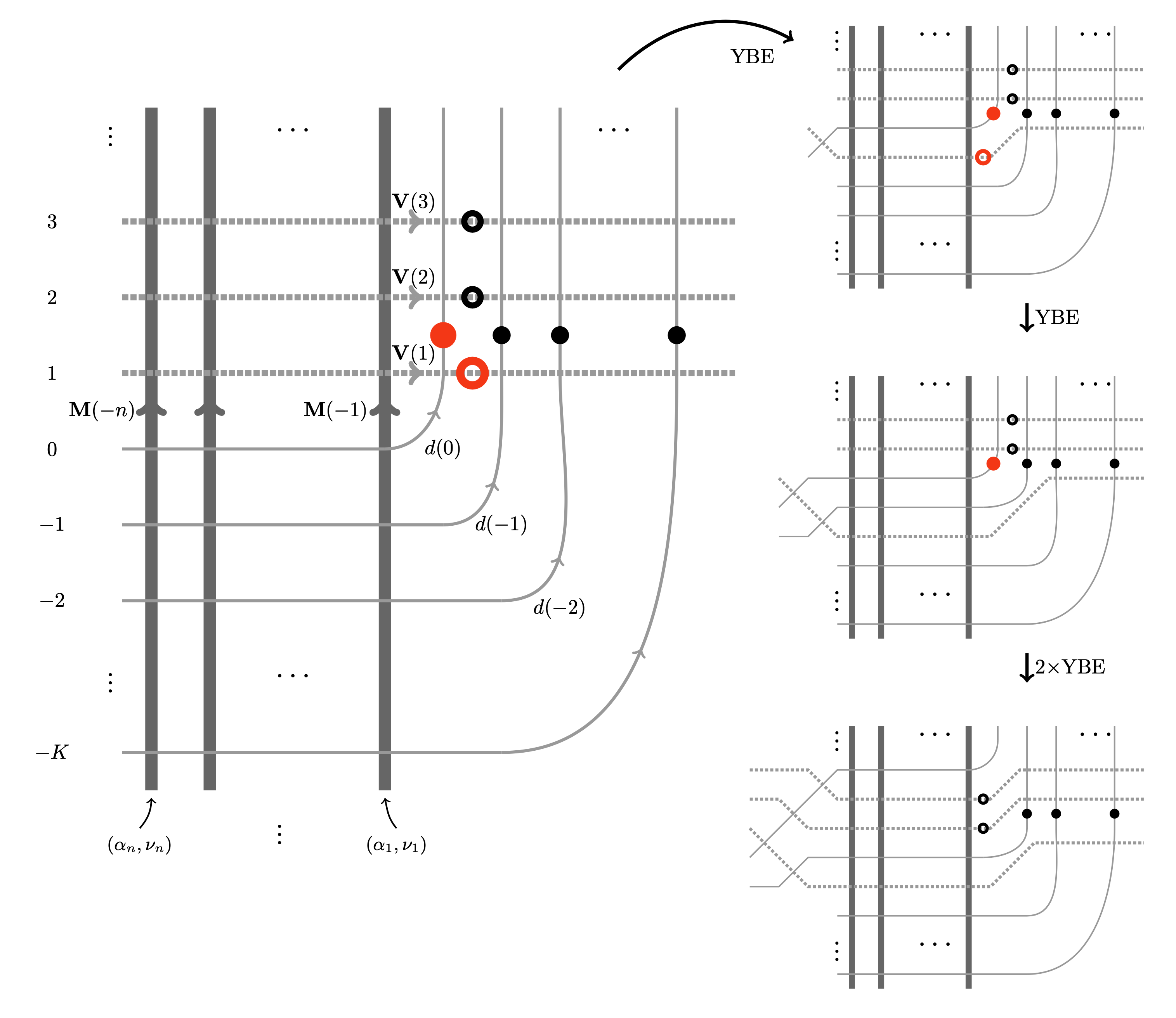
  1. Svetlana Gavrilova, Leonid Petrov. Tilted biorthogonal ensembles, Grothendieck random partitions, and determinantal tests (2023) • Selecta Math. (2024), Volume 30, article 56 • arXiv:2305.17747 [math.PR] • (PDF) • (TeX)
    Abstract

    We study probability measures on partitions based on symmetric Grothendieck polynomials. These deformations of Schur polynomials introduced in the K-theory of Grassmannians share many common properties. Our Grothendieck measures are analogs of the Schur measures on partitions introduced by Okounkov (1999). Despite the similarity of determinantal formulas for the probability weights of Schur and Grothendieck measures, we demonstrate that Grothendieck measures are \emph{not} determinantal point processes. This question is related to the principal minor assignment problem in algebraic geometry, and we employ a determinantal test first obtained by Nanson in 1897 for the $4\times4$ problem. We also propose a procedure for getting Nanson-like determinantal tests for matrices of any size $n\ge4$ which appear new for $n\ge 5$.

    By placing the Grothendieck measures into a new framework of tilted biorthogonal ensembles generalizing a rich class of determinantal processes introduced by Borodin (1998), we identify Grothendieck random partitions as a cross-section of a Schur process, a determinantal process in two dimensions. This identification expresses the correlation functions of Grothendieck measures through sums of Fredholm determinants, which are not immediately suitable for asymptotic analysis. A more direct approach allows us to obtain a limit shape result for the Grothendieck random partitions. The limit shape curve is not particularly explicit as it arises as a cross-section of the limit shape surface for the Schur process. The gradient of this surface is expressed through the argument of a complex root of a cubic equation.

    Limit shapes of 2d Schur processes and the corresponding Grothendieck random partitions
  2. Leonid Petrov, Mikhail Tikhonov. Asymptotics of noncolliding q-exchangeable random walks (2023) • J. Phys. A: Math. Theor. 56 365203 • arXiv:2303.02380 [math.PR] • (PDF)
    Abstract

    We consider a process of noncolliding $q$-exchangeable random walks on $\mathbb{Z}$ making steps $0$ (straight) and $-1$ (down). A single random walk is called $q$-exchangeable if under an elementary transposition of the neighboring steps $ (\textnormal{down},\textnormal{straight}) \to (\textnormal{straight}, \textnormal{down}) $ the probability of the trajectory is multiplied by a parameter $q\in(0,1)$. Our process of $m$ noncolliding $q$-exchangeable random walks is obtained from the independent $q$-exchangeable walks via the Doob’s $h$-transform for a certain nonnegative eigenfunction $h$ with the eigenvalue less than $1$. The system of $m$ walks evolves in the presence of an absorbing wall at $0$.

    We show that the trajectory of the noncolliding $q$-exchangeable walks started from an arbitrary initial configuration forms a determinantal point process, and express its kernel in a double contour integral form. This kernel is obtained as a limit from the correlation kernel of $q$-distributed random lozenge tilings of sawtooth polygons.

    In the limit as $m\to \infty$, $q=e^{-\gamma/m}$ with $\gamma>0$ fixed, and under a suitable scaling of the initial data, we obtain a limit shape of our noncolliding walks and also show that their local statistics are governed by the incomplete beta kernel. The latter is a distinguished translation invariant ergodic extension of the two-dimensional discrete sine kernel.

    Limit shapes of the noncolliding q-exchangeable random walks
  3. Leonid Petrov, Axel Saenz. Rewriting History in Integrable Stochastic Particle Systems (2022) • Commun. Math. Phys., 405 (300), 2024. • arXiv:2212.01643 [math.PR] • (PDF) • (TeX)
    Abstract

    Many integrable stochastic particle systems in one space dimension (such as TASEP — Totally Asymmetric Simple Exclusion Process — and its $q$-deformation, the $q$-TASEP) remain integrable if we equip each particle with its own speed parameter. In this work, we present intertwining relations between Markov transition operators of particle systems which differ by a permutation of the speed parameters. These relations generalize our previous works [1], [2], but here we employ a novel approach based on the Yang-Baxter equation for the higher spin stochastic six vertex model. Our intertwiners are Markov transition operators, which leads to interesting probabilistic consequences.

    First, we obtain a new Lax-type differential equation for the Markov transition semigroups of homogeneous, continuous-time versions of our particle systems. Our Lax equation encodes the time evolution of multipoint observables of the $q$-TASEP and TASEP in a unified way, which may be of interest for the asymptotic analysis of multipoint observables of these systems.

    Second, we show that our intertwining relations lead to couplings between probability measures on trajectories of particle systems which differ by a permutation of the speed parameters. The conditional distribution for such a coupling is realized as a “rewriting history” random walk which randomly resamples the trajectory of a particle in a chamber determined by the trajectories of the neighboring particles. As a byproduct, we construct a new coupling for standard Poisson processes on the positive real half-line with different rates.

    A poem on the topic

    by OpenAI

    In stochastic particle systems, there’s a way
    To rewrite history with each passing day.
    A single particle, its fate made clear,
    Can undo what’s been done and make it reappear.

    The laws of probability and chaos at play
    Can be bent to our will, if we but obey.
    The deterministic systems in our control,
    Will yield to a new order, as it starts to unfold.

    The particles and their interactions will dictate,
    The outcome of our systems, no matter their state.
    With the tools of integrability, we can rewrite,
    The future of our systems with a single bite.

    Two-car systems with cars of different speeds. In every picture, the blue and the yellow trajectories are of the faster and the slower cars, respectively. <br><b>Top</b>: cars start at neighboring locations, and the trajectory of the second car, $x_2(t)$, is the same in distribution. <br><b>Bottom</b>: cars start at locations away from each other, and the distributions of the trajectories of the second car are different in the left and the central pictures. However, when we randomize the initial condition, the distribution of the second car in the slow-fast system with the randomized initial condition is the same as in the fast-slow system on the left.
  4. Leonid Petrov. Noncolliding Macdonald walks with an absorbing wall (2022) • SIGMA 18 (2022), 079, 21 pages • arXiv:2204.09206 [math.PR] • (PDF)
    Abstract

    The branching rule is one of the most fundamental properties of the Macdonald symmetric polynomials. It expresses a Macdonald polynomial as a nonnegative linear combination of Macdonald polynomials with smaller number of variables. Taking a limit of the branching rule under the principal specialization when the number of variables goes to infinity, we obtain a Markov chain of $m$ noncolliding particles with negative drift and an absorbing wall at zero. The chain depends on the Macdonald parameters $(q,t)$ and may be viewed as a discrete deformation of the Dyson Brownian motion. The trajectory of the Markov chain is equivalent to a certain Gibbs ensemble of plane partitions with an arbitrary cascade front wall.

    In the Jack limit $q=t^{\beta/2}\to1$ the absorbing wall disappears, and the Macdonald noncolliding walks turn into the $\beta$-noncolliding random walks studied by Huang [arXiv:1708.07115]. Taking $q=0$ (Hall-Littlewood degeneration) and further sending $t\to 1$, we obtain a continuous time particle system on $\mathbb{Z}_{\ge0}$ with inhomogeneous jump rates and absorbing wall at zero.

    Noncolliding walks, lozenge tilings, and plane partitions
  5. Matthew Nicoletti, Leonid Petrov. Irreversible Markov Dynamics and Hydrodynamics for KPZ States in the Stochastic Six Vertex Model (2022) • Electronic Journal of Probability 2023, Vol. 28, paper no. 138, 1-55. • arXiv:2201.12497 [math.PR] • (PDF) • (TeX)
    Abstract

    We introduce a family of Markov growth processes on discrete height functions defined on the 2-dimensional square lattice. Each height function corresponds to a configuration of the six vertex model on the infinite square lattice. We focus on the stochastic six vertex model corresponding to a particular two-parameter family of weights within the ferroelectric regime. It is believed (and partially proven, see Aggarwal, arXiv:2004.13272) that the stochastic six vertex model displays nontrivial pure (i.e., translation invariant and ergodic) Gibbs states of two types, KPZ and liquid. These phases have very different long-range correlation structure. The Markov processes we construct preserve the KPZ pure states in the full plane. We also show that the same processes put on the torus preserve arbitrary Gibbs measures for generic six vertex weights (not necessarily in the ferroelectric regime).

    Our dynamics arise naturally from the Yang-Baxter equation for the six vertex model via its bijectivisation, a technique first used in Bufetov-Petrov (arXiv:1712.04584). The dynamics we construct are irreversible; in particular, the height function has a nonzero average drift. In each KPZ pure state, we explicitly compute the average drift (also known as the current) as a function of the slope. We use this to analyze the hydrodynamics of a non-stationary version of our process acting on quarter plane stochastic six vertex configurations. The fixed-time limit shapes in the quarter plane model were obtained in Borodin-Corwin-Gorin (arXiv:1407.6729).

    The twisted torus, a six vertex configuration, and the corresponding height function
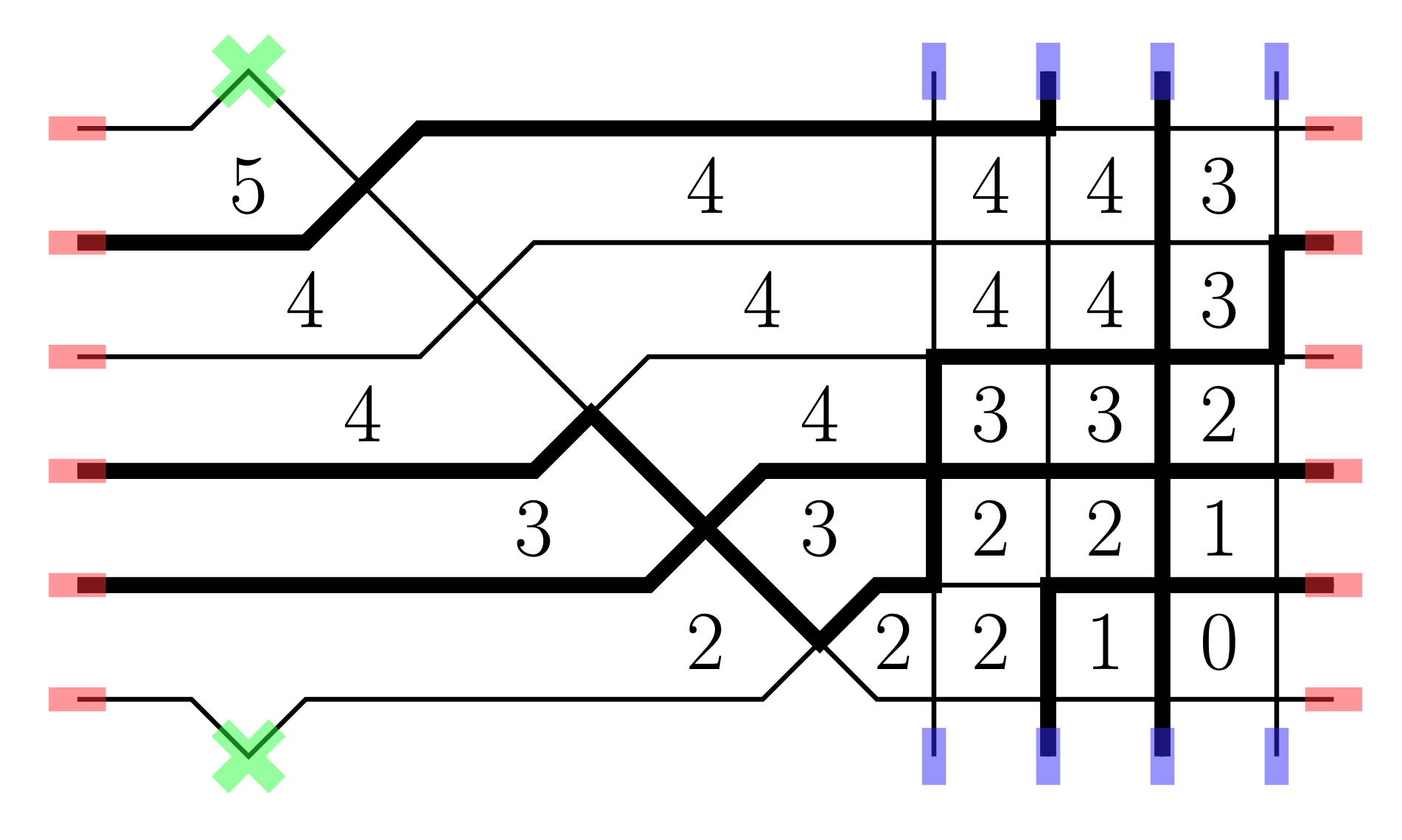
  6. Amol Aggarwal, Alexei Borodin, Leonid Petrov, Michael Wheeler. Free Fermion Six Vertex Model: Symmetric Functions and Random Domino Tilings (2021) • Selecta Math., 29, article 36 (2023) • arXiv:2109.06718 [math.PR] • (PDF)
    Abstract

    Our work deals with symmetric rational functions and probabilistic models based on the fully inhomogeneous six vertex (ice type) model satisfying the free fermion condition. Two families of symmetric rational functions $F_\lambda,G_\lambda$ are defined as certain partition functions of the six vertex model, with variables corresponding to row rapidities, and the labeling signatures $\lambda=(\lambda_1\ge \ldots\ge \lambda_N)\in \mathbb{Z}^N$ encoding boundary conditions. These symmetric functions generalize Schur symmetric polynomials, as well as some of their variations, such as factorial and supersymmetric Schur polynomials. Cauchy type summation identities for $F_\lambda,G_\lambda$ and their skew counterparts follow from the Yang–Baxter equation. Using algebraic Bethe Ansatz, we obtain a double alternant type formula for $F_\lambda$ and a Sergeev–Pragacz type formula for $G_\lambda$.

    In the spirit of the theory of Schur processes, we define probability measures on sequences of signatures with probability weights proportional to products of our symmetric functions. We show that these measures can be viewed as determinantal point processes, and we express their correlation kernels in a double contour integral form. We present two proofs: The first is a direct computation of Eynard–Mehta type, and the second uses non-standard, inhomogeneous versions of fermionic operators in a Fock space coming from the algebraic Bethe Ansatz for the six vertex model.

    We also interpret our determinantal processes as random domino tilings of a half-strip with inhomogeneous domino weights. In the bulk, we show that the lattice asymptotic behavior of such domino tilings is described by a new determinantal point process on $\mathbb{Z}^{2}$, which can be viewed as an doubly-inhomogeneous generalization of the extended discrete sine process.

    An example of a domino tiling with inhomogeneous weights which we treat in this paper
  7. Leonid Petrov. Refined Cauchy identity for spin Hall-Littlewood symmetric rational functions (2020) • Journal of Combinatorial Theory Ser. A, vol. 184 (2021), 105519 • arXiv:2007.10886 [math.CO] • (PDF) • (TeX)
    Abstract

    Fully inhomogeneous spin Hall-Littlewood symmetric rational functions \(\mathsf{F}_\lambda\) arise in the context of $\mathfrak{sl}(2)$ higher spin six vertex models, and are multiparameter deformations of the classical Hall-Littlewood symmetric polynomials. We obtain a refined Cauchy identity expressing a weighted sum of the product of two $\mathsf{F}_\lambda$’s as a determinant. The determinant is of Izergin-Korepin type: it is the partition function of the six vertex model with suitably decorated domain wall boundary conditions. The proof of equality of two partition functions is based on the Yang-Baxter equation.

    We rewrite our Izergin-Korepin type determinant in a different form which includes one of the sets of variables in a completely symmetric way. This determinantal identity might be of independent interest, and also allows to directly link the spin Hall-Littlewood rational functions with (the Hall-Littlewood particular case of) the interpolation Macdonald polynomials. In a different direction, a Schur expansion of our Izergin-Korepin type determinant yields a deformation of Schur symmetric polynomials.

    In the spin-$\frac12$ specialization, our refined Cauchy identity leads to a summation identity for eigenfunctions of the ASEP (Asymmetric Simple Exclusion Process), a celebrated stochastic interacting particle system in the Kardar-Parisi-Zhang universality class. This produces explicit integral formulas for certain multitime probabilities in ASEP.

    Two lattices with equal partition functions. This leads to a refined Cauchy identity
  8. Matteo Mucciconi, Leonid Petrov. Spin q-Whittaker polynomials and deformed quantum Toda (2020) • Communications in Mathematical Physics, 389, pages 1331-1416 (2022) • arXiv:2003.14260 [math.PR] • (PDF) • (TeX)
    Abstract

    Spin $q$-Whittaker symmetric polynomials labeled by partitions $\lambda$ were recently introduced by Borodin and Wheeler (arXiv:1701.06292) in the context of integrable $\mathfrak{sl}_2$ vertex models. They are a one-parameter deformation of the $t=0$ Macdonald polynomials. We present a new, more convenient modification of spin $q$-Whittaker polynomials and find two Macdonald type $q$-difference operators acting diagonally in these polynomials with eigenvalues, respectively, $q^{-\lambda_1}$ and $q^{\lambda_N}$ (where $\lambda$ is the polynomial’s label). We study probability measures on interlacing arrays based on spin $q$-Whittaker polynomials, and match their observables with known stochastic particle systems such as the $q$-Hahn TASEP.

    In a scaling limit as $q\nearrow 1$, spin $q$-Whittaker polynomials turn into a new one-parameter deformation of the $\mathfrak{gl}_n$ Whittaker functions. The rescaled Pieri type rule gives rise to a one-parameter deformation of the quantum Toda Hamiltonian. The deformed Hamiltonian acts diagonally on our new spin Whittaker functions. On the stochastic side, as $q\nearrow 1$ we discover a multilevel extension of the beta polymer model of Barraquand and Corwin (arXiv:1503.04117), and relate it to spin Whittaker functions.

    The new deformed quantum Toda Hamiltonian
  9. Leonid Petrov, Mikhail Tikhonov. Parameter symmetry in perturbed GUE corners process and reflected drifted Brownian motions (2019) • Journal of Statistical Physics, 181 (2020), 1996-2010 • arXiv:1912.08671 [math.PR] • (PDF)
    Abstract

    The perturbed GUE corners ensemble is the joint distribution of eigenvalues of all principal submatrices of a matrix $G+\mathrm{diag}(\mathbf{a})$, where $G$ is the random matrix from the Gaussian Unitary Ensemble (GUE), and $\mathrm{diag}(\mathbf{a})$ is a fixed diagonal matrix. We introduce Markov transitions based on exponential jumps of eigenvalues, and show that their successive application is equivalent in distribution to a deterministic shift of the matrix. This result also leads to a new distributional symmetry for a family of reflected Brownian motions with drifts coming from an arithmetic progression.

    The construction we present may be viewed as a random matrix analogue of the recent results of the first author and Axel Saenz.

    A poem on the topic

    by OpenAI

    The corners of random matrices
    Grow with a sudden twist
    Their perturbations form an ellipse
    A strange and curious list

    The reflected drift of Brownian motions
    Goes to and fro in space
    A symmetry of random walks
    A curious thing to trace

    The paths of randomness and chance
    Rise and fall and weave
    But in their changing patterns
    A pattern of reprieve

    Is found in the randomness of their paths
    A mathematical game
    The symmetry of perturbed GUE corners
    And reflected drifted Brownian motion the same

    Perturbed Dyson Brownian motion - eigenvalue dynamics of a 6x6 matrix of Brownian motions, with no drift off the diagonal, and an arithmetic progression of drifts on the diagonal
  10. Leonid Petrov. Parameter permutation symmetry in particle systems and random polymers (2019) • SIGMA 17 (2021), 021, 34 pages • arXiv:1912.06067 [math.PR]
    Abstract

    Many integrable stochastic particle systems in one space dimension (such as TASEP - Totally Asymmetric Simple Exclusion Process - and its various deformations, with a notable exception of ASEP) remain integrable when we equip each particle $x_i$ with its own jump rate parameter $\nu_i$. It is a consequence of integrability that the distribution of each particle $x_n(t)$ in a system started from the step initial configuration depends on the parameters $\nu_j$, $j\le n$, in a symmetric way. A transposition $\nu_n \leftrightarrow \nu_{n+1}$ of the parameters thus affects only the distribution of $x_n(t)$. For $q$-Hahn TASEP and its degenerations (namely, $q$-TASEP and beta polymer) we realize the transposition $\nu_n \leftrightarrow \nu_{n+1}$ as an explicit Markov swap operator acting on the single particle $x_n(t)$. For beta polymer, the swap operator can be interpreted as a simple modification of the lattice on which the polymer is considered. Our main tools are Markov duality and contour integral formulas for joint moments.

    In particular, our constructions lead to a continuous time Markov process $\mathsf{Q}^{(\mathsf{t})}$ preserving the time $\mathsf{t}$ distribution of the $q$-TASEP (with step initial configuration, where $\mathsf{t}\in \mathbb{R}_{>0}$ is fixed). The dual system is a certain transient modification of the stochastic $q$-Boson system. We identify asymptotic survival probabilities of this transient process with $q$-moments of the $q$-TASEP, and use this to show convergence of the process $\mathsf{Q}^{(\mathsf{t})}$ with arbitrary initial data to its stationary distribution.

    Setting $q=0$, we recover the results about the usual TASEP established recently in this paper by a different approach based on Gibbs ensembles of interlacing particles in two dimensions.

    Modification of the lattice leading to the elimination of parameters of the beta polymer
  11. Leonid Petrov. PushTASEP in inhomogeneous space (2019) • Electronic Journal of Probability, vol. 25 (2020), paper no. 114 • arXiv:1910.08994 [math.PR]
    Abstract

    We consider the PushTASEP (pushing totally asymmetric simple exclusion process, also sometimes called long-range TASEP) with the step initial configuration evolving in an inhomogeneous space. That is, the rate of each particle’s jump depends on the location of this particle. We match the distribution of the height function of this PushTASEP with Schur processes. Using this matching and determinantal structure of Schur processes, we obtain limit shape and fluctuation results which are typical for stochastic particle systems in the Kardar-Parisi-Zhang universality class. PushTASEP is a close relative of the usual TASEP. In inhomogeneous space the former is integrable, while the integrability of the latter is not known.

    Limit shapes in inhomogeneous PushTASEP
  12. Leonid Petrov, Axel Saenz. Mapping TASEP back in time (2019) • Probability Theory and Related Fields, 182, pages 481-530 (2022) • arXiv:1907.09155 [math.PR] • (PDF)
    Abstract

    We obtain a new relation between the distributions $\mu_t$ at different times $t\ge 0$ of the continuous-time TASEP (Totally Asymmetric Simple Exclusion Process) started from the step initial configuration. Namely, we present a continuous-time Markov process with local interactions and particle-dependent rates which maps the TASEP distributions $\mu_t$ backwards in time. Under the backwards process, particles jump to the left, and the dynamics can be viewed as a version of the discrete-space Hammersley process. Combined with the forward TASEP evolution, this leads to an stationary Markov dynamics preserving $\mu_t$ which in turn brings new identities for expectations with respect to $\mu_t$.

    The construction of the backwards dynamics is based on Markov maps interchanging parameters of Schur processes, and is motivated by bijectivizations of the Yang-Baxter equation. We also present a number of corollaries, extensions, and open questions arising from our constructions.

    Multitime distribution in the backwards Hammersley-type process
  13. Alexey Bufetov, Matteo Mucciconi, Leonid Petrov. Yang-Baxter random fields and stochastic vertex models (2019) • Advances in Mathematics 388 (2021), 107865 • arXiv:1905.06815 [math.PR] • (TeX)
    Abstract

    Bijectivization refines the Yang-Baxter equation into a pair of local Markov moves which randomly update the configuration of the vertex model. Employing this approach, we introduce new Yang-Baxter random fields of Young diagrams based on spin $q$-Whittaker and spin Hall-Littlewood symmetric functions. We match certain scalar Markovian marginals of these fields with (1) the stochastic six vertex model; (2) the stochastic higher spin six vertex model; and (3) a new vertex model with pushing which generalizes the $q$-Hahn PushTASEP introduced recently by Corwin-Matveev-Petrov (2018). Our matchings include models with two-sided stationary initial data, and we obtain Fredholm determinantal expressions for the $q$-Laplace transforms of the height functions of all these models. Moreover, we also discover difference operators acting diagonally on spin $q$-Whittaker or (stable) spin Hall-Littlewood symmetric functions.

    Yang-Baxter equation and its bijectivisation
  14. Ivan Corwin, Konstantin Matveev, Leonid Petrov. The q-Hahn PushTASEP (2018) • International Mathematics Research Notices (2019), rnz106 • arXiv:1811.06475 [math.PR]
    Abstract

    We introduce the $q$-Hahn PushTASEP — an integrable stochastic interacting particle system which is a 3-parameter generalization of the PushTASEP, a well-known close relative of the TASEP (Totally Asymmetric Simple Exclusion Process). The transition probabilities in the $q$-Hahn PushTASEP are expressed through the $_4\phi_3$ basic hypergeometric function. Under suitable limits, the $q$-Hahn PushTASEP degenerates to all known integrable (1+1)-dimensional stochastic systems with a pushing mechanism. One can thus view our new system as a pushing counterpart of the $q$-Hahn TASEP introduced by Povolotsky. We establish Markov duality relations and contour integral formulas for the $q$-Hahn PushTASEP. We also take a $q\to1$ limit of our process arriving at a new beta polymer-like model.

    The q-Hahn PushTASEP
  15. Alisa Knizel, Leonid Petrov, Axel Saenz. Generalizations of TASEP in discrete and continuous inhomogeneous space (2018) • Communications in Mathematical Physics 372 (2019), no. 3, pp 797-864 • arXiv:1808.09855 [math.PR] • (PDF) • (TeX)
    Abstract

    We investigate a rich new class of exactly solvable particle systems generalizing the Totally Asymmetric Simple Exclusion Process (TASEP). Our particle systems can be thought of as new exactly solvable examples of tandem queues, directed first- or last passage percolation models, or Robinson-Schensted-Knuth type systems with random input. One of the novel features of the particle systems is the presence of spatial inhomogeneity which can lead to the formation of traffic jams.

    For systems with special step-like initial data, we find explicit limit shapes, describe hydrodynamic evolution, and obtain asymptotic fluctuation results which put the systems into the Kardar-Parisi-Zhang universality class. At a critical scaling around a traffic jam in the continuous space TASEP, we observe deformations of the Tracy-Widom distribution and the extended Airy kernel, revealing the finer structure of this novel type of phase transitions.

    A homogeneous version of a discrete space system we consider is a one-parameter deformation of the geometric last passage percolation, and we obtain extensions of the limit shape parabola and the corresponding asymptotic fluctuation results.

    The exact solvability and asymptotic behavior results are powered by a new nontrivial connection to Schur measures and processes.

    Emergence of a discontinuity of the height function at a slowdown
  16. Christian Gromoll, Mark Meckes, Leonid Petrov. Quenched Central Limit Theorem in a Corner Growth Setting (2018) • Electronic Communications in Probability (2018), Vol. 23, paper no. 101, 1-12 • arXiv:1804.04222 [math.PR]
    Abstract

    We consider point-to-point directed paths in a random environment on the two-dimensional integer lattice. For a general independent environment under mild assumptions we show that the quenched energy of a typical path satisfies a central limit theorem as the mesh of the lattice goes to zero. Our proofs rely on concentration of measure techniques and some combinatorial bounds on families of paths.

    A histogram of the path energies ‐ the original motivation for the work
  17. Alexey Bufetov, Leonid Petrov. Yang-Baxter field for spin Hall-Littlewood symmetric functions (2017) • Forum of Mathematics Sigma 7 (2019), e39 • arXiv:1712.04584 [math.PR] • (PDF) • (TeX)
    Abstract

    Employing bijectivisation of summation identities, we introduce local stochastic moves based on the Yang-Baxter equation for . Combining these moves leads to a new object which we call the spin Hall-Littlewood Yang-Baxter field - a probability distribution on two-dimensional arrays of particle configurations on the discrete line. We identify joint distributions along down-right paths in the Yang-Baxter field with spin Hall-Littlewood processes, a generalization of Schur processes. We consider various degenerations of the Yang-Baxter field leading to new dynamic versions of the stochastic six vertex model and of the Asymmetric Simple Exclusion Process.

    A poem on the topic

    by OpenAI

    The stars aloft their burning lamps display,
    To light the paths of night away;
    And yonder in the Yang-Baxter field,
    The spin Hall-Littlewood symmetric yield.

    The symmetry of night, so grand and fair,
    Is held in harmony by the square;
    And in its own eternal way,
    Shines forth in every spin Hall day.

    The spin Hall-Littlewood symmetric stay,
    In constancy through night and day;
    In every corner of the sky,
    It stands unshaken, bold and high.

    The stars above are ever bright,
    Their symmetry is ever right;
    The spin Hall-Littlewood symmetric yield
    Shines in the Yang-Baxter field.

    Forward transition probabilities associated with the Yang-Baxter field
  18. Michael Damron, Leonid Petrov, David Sivakoff. Coarsening model on Zd with biased zero-energy flips and an exponential large deviation bound for ASEP (2017) • Communications in Mathematical Physics 362 (2018), no. 1, 185-217 • arXiv:1708.05806 [math.PR]
    Abstract

    We study the coarsening model (zero-temperature Ising Glauber dynamics) on $\mathbb{Z}^d$ (for $d \geq 2$) with an asymmetric tie-breaking rule. This is a Markov process on the state space ${-1,+1}^{\mathbb{Z}^d}$ of “spin configurations” in which each vertex updates its spin to agree with a majority of its neighbors at the arrival times of a Poisson process. If a vertex has equally many $+1$ and $-1$ neighbors, then it updates its spin value to $+1$ with probability $q \in [0,1]$ and to $-1$ with probability $1-q$. The initial state of this Markov chain is distributed according to a product measure with probability $p$ for a spin to be $+1$.

    In this paper, we show that for any given $p>0$, there exist $q$ close enough to 1 such that a.s. every spin has a limit of $+1$. This is of particular interest for small values of $p$, for which it is known that if $q=1/2$, a.s. all spins have a limit of $-1$. For dimension $d=2$, we also obtain near-exponential convergence rates for $q$ sufficiently large, and for general $d$, we obtain stretched exponential rates independent of $d$. Two important ingredients in our proofs are refinements of block arguments of Fontes-Schonmann-Sidoravicius and a novel exponential large deviation bound for the Asymmetric Simple Exclusion Process.

    A poem on the topic

    by OpenAI

    I

    A model on Zd with biased flips,
    A balancing of zeroes and tips,
    A measure of lops and shifts,
    An exponential large deviation bound,
    For a one-dimensional ASEP profound.

    II

    The coarsening of the system is seen,
    As the particles move and the zeroes lean,
    The bias of the flips can be seen too,
    As the ASEP system evolves and grows anew.

    III

    The large deviation bound to prove,
    The ASEP is stationary and will move,
    The bias in the flips and the zeroes,
    Is the key to the dynamics of the system, and its foes.

    IV

    The coarsening model on Zd,
    With its biased flips and exponential bounds,
    Will be the key to understanding,
    The ASEP dynamics and its expanding.

    This is how the GUE Tracy-Widom/Airy$_2$ double critical point is deformed in our large deviations regime. In this case the double critical point is split into two real critical points, and the large deviations function comes from the difference between the values of $S(\cdot)$ at these two new points
  19. Sevak Mkrtchyan, Leonid Petrov. GUE corners limit of q-distributed lozenge tilings (2017) • Electronic Journal of Probability, Volume 22 (2017), paper no. 101, 24 pp • arXiv:1703.07503 [math.PR]
    Abstract

    We study asymptotics of $q$-distributed random lozenge tilings of sawtooth domains (equivalently, of random interlacing integer arrays with fixed top row). Under the distribution we consider each tiling is weighted proportionally to $q^{\mathsf{vol}}$, where $\mathsf{vol}$ is the volume under the corresponding 3D stepped surface. We prove the following Interlacing Central Limit Theorem: as $q\rightarrow1$, the domain gets large, and the fixed top row approximates a given nonrandom profile, the vertical lozenges are distributed as the eigenvalues of a GUE random matrix and of its successive principal corners. Our results extend the GUE corners asymptotics for tilings of bounded polygonal domains previously known in the uniform (i.e., $q=1$) case. Even though $q$ goes to $1$, the presence of the $q$-weighting affects non-universal constants in our Central Limit Theorem.

    Region where one sees the GUE statistics
  20. Alexei Borodin, Leonid Petrov. Inhomogeneous exponential jump model (2017) • Probability Theory and Related Fields 172 (2018), 323-385 • arXiv:1703.03857 [math.PR]
    Abstract

    We introduce and study the inhomogeneous exponential jump model — an integrable stochastic interacting particle system on the continuous half line evolving in continuous time. An important feature of the system is the presence of arbitrary spatial inhomogeneity on the half line which does not break the integrability. We completely characterize the macroscopic limit shape and asymptotic fluctuations of the height function (= integrated current) in the model. In particular, we explain how the presence of inhomogeneity may lead to macroscopic phase transitions in the limit shape such as shocks or traffic jams. Away from these singularities the asymptotic fluctuations of the height function around its macroscopic limit shape are governed by the GUE Tracy–Widom distribution. A surprising result is that while the limit shape is discontinuous at a traffic jam caused by a macroscopic slowdown in the inhomogeneity, fluctuations on both sides of such a traffic jam still have the GUE Tracy–Widom distribution (but with different non-universal normalizations).

    The integrability of the model comes from the fact that it is a degeneration of the inhomogeneous stochastic higher spin six vertex models studied earlier in arXiv:1601.05770 [math.PR].

    Limit shape and fluctuations in the inhomogeneous exponential jump model
  21. Daniel Orr, Leonid Petrov. Stochastic higher spin six vertex model and q-TASEPs (2016) • Advances in Mathematics 317 (2017), 473-525 • arXiv:1610.10080 [math.PR]
    Abstract

    We present two new connections between the inhomogeneous stochastic higher spin six vertex model in a quadrant and integrable stochastic systems from the Macdonald processes hierarchy.

    First, we show how Macdonald $q$-difference operators with $t=0$ (an algebraic tool crucial for studying the corresponding Macdonald processes) can be utilized to get $q$-moments of the height function $\mathfrak{h}$ in the higher spin six vertex model first computed in arXiv:1601.05770 [math.PR] using Bethe ansatz. This result in particular implies that for the vertex model with the step Bernoulli boundary condition, the value of $\mathfrak{h}$ at an arbitrary point has the same distribution as the last component $\lambda_N$ of a random partition under a specific $t=0$ Macdonald measure.

    On the other hand, it is known that $\mathbf{x}_N:=\lambda_N-N$ can be identified with the location of the $N$th particle in a certain discrete time $q$-TASEP started from the step initial configuration. The second construction we present is a coupling of this $q$-TASEP and the higher spin six vertex model (with the step Bernoulli boundary condition) along time-like paths providing an independent probabilistic explanation of the equality of $\mathfrak{h}(N+1,T)$ and $\mathbf{x}_N+N$ in distribution. Combined with the identification of averages of observables between the stochastic higher spin six vertex model and Schur measures (which are $t=q$ Macdonald measures) obtained recently in arXiv:1608.01553 [math-ph], this produces GUE Tracy–Widom asymptotics for a discrete time $q$-TASEP with the step initial configuration and special jump parameters.

    Coupling of q-TASEPs and the stochastic higher spin six vertex model
  22. Vadim Gorin, Leonid Petrov. Universality of local statistics for noncolliding random walks (2016) • Annals of Probability (2019), Vol. 47, No. 5, 2686-2753 • arXiv:1608.03243 [math.PR] • (PDF)
    Abstract

    We consider the $N$-particle noncolliding Bernoulli random walk — a discrete time Markov process in $\mathbb{Z}^{N}$ obtained from a collection of $N$ independent simple random walks with steps $\in{0,1}$ by conditioning that they never collide. We study the asymptotic behavior of local statistics of this process started from an arbitrary initial configuration on short times $T\ll N$ as $N\to+\infty$. We show that if the particle density of the initial configuration is bounded away from $0$ and $1$ down to scales $\mathsf{D}\ll T$ in a neighborhood of size $\mathsf{Q}\gg T$ of some location $x$ (i.e., $x$ is in the ``bulk’’), and the initial configuration is balanced in a certain sense, then the space-time local statistics at $x$ are asymptotically governed by the extended discrete sine process (which can be identified with a translation invariant ergodic Gibbs measure on lozenge tilings of the plane). We also establish similar results for certain types of random initial data. Our proofs are based on a detailed analysis of the determinantal correlation kernel for the noncolliding Bernoulli random walk.

    The noncolliding Bernoulli random walk is a discrete analogue of the Dyson Brownian Motion whose local statistics are universality governed by the continuous sine process. Our results parallel the ones in the continuous case. In addition, we naturally include situations with inhomogeneous local particle density on scale $T$, which nontrivially affects parameters of the limiting extended sine process, and in a particular case leads to a new behavior.

    Noncolliding Bernoulli random walks
  23. Alexei Borodin, Leonid Petrov. Lectures on Integrable probability: Stochastic vertex models and symmetric functions (2016) • Lecture Notes of the Les Houches Summer School, Volume 104, July 2015 • arXiv:1605.01349 [math.PR]
    Abstract

    We consider a homogeneous stochastic higher spin six vertex model in a quadrant. For this model we derive concise integral representations for multi-point q-moments of the height function and for the q-correlation functions. At least in the case of the step initial condition, our formulas degenerate in appropriate limits to many known formulas of such type for integrable probabilistic systems in the (1+1)d KPZ universality class, including the stochastic six vertex model, ASEP, various q-TASEPs, and associated zero range processes.

    Our arguments are largely based on properties of a family of symmetric rational functions (introduced in arXiv:1410.0976 [math.CO]) that can be defined as partition functions of the higher spin six vertex model for suitable domains; they generalize classical Hall-Littlewood and Schur polynomials. A key role is played by Cauchy-like summation identities for these functions, which are obtained as a direct corollary of the Yang-Baxter equation for the higher spin six vertex model.

    These are lecture notes for a course given by A.B. at the Ecole de Physique des Houches in July of 2015. All the results and proofs presented here generalize to the setting of the fully inhomogeneous higher spin six vertex model, see arXiv:1601.05770 [math.PR] for a detailed exposition of the inhomogeneous case.

    Creation operator in a Bethe ansatz representation
  24. Alexei Borodin, Leonid Petrov. Higher spin six vertex model and symmetric rational functions (2016) • Selecta Mathematica 24 (2018), no. 2, 751-874 • arXiv:1601.05770 [math.PR]
    Abstract

    We consider a fully inhomogeneous stochastic higher spin six vertex model in a quadrant. For this model we derive concise integral representations for multi-point q-moments of the height function and for the q-correlation functions. At least in the case of the step initial condition, our formulas degenerate in appropriate limits to many known formulas of such type for integrable probabilistic systems in the (1+1)d KPZ universality class, including the stochastic six vertex model, ASEP, various q-TASEPs, and associated zero range processes.

    Our arguments are largely based on properties of a family of symmetric rational functions which can be defined as partition functions of the inhomogeneous higher spin six vertex model for suitable domains. In the homogeneous case, such functions were previously studied in arXiv:1410.0976 [math.CO]; they also generalize classical Hall-Littlewood and Schur polynomials. A key role is played by Cauchy-like summation identities for these functions, which are obtained as a direct corollary of the Yang-Baxter equation for the higher spin six vertex model.

    inhomogeneous stochastic six vertex model
  25. Konstantin Matveev, Leonid Petrov. q-randomized Robinson-Schensted-Knuth correspondences and random polymers (2015) • Annales de l'Institut Henri Poincare D: Combinatorics, Physics and their Interactions 4 (2017), no. 1, 1-123 • arXiv:1504.00666 [math.PR]
    Abstract

    We introduce and study $q$-randomized Robinson-Schensted-Knuth (RSK) correspondences which interpolate between the classical ($q=0$) and geometric ($q\to 1$) RSK correspondences (the latter ones are sometimes also called tropical).

    For $0< q <1$ our correspondences are randomized, i.e., the result of an insertion is a certain probability distribution on semistandard Young tableaux. Because of this randomness, we use the language of discrete time Markov dynamics on two-dimensional interlacing particle arrays (these arrays are in a natural bijection with semistandard tableaux). Our dynamics act nicely on a certain class of probability measures on arrays, namely, on $q$-Whittaker processes (which are $t=0$ versions of Macdonald processes). We present four Markov dynamics which for $q=0$ reduce to the classical row or column RSK correspondences applied to a random input matrix with independent geometric or Bernoulli entries.

    Our new two-dimensional discrete time dynamics generalize and extend several known constructions: (1) The discrete time $q$-TASEPs arise as one-dimensional marginals of our “column” dynamics. In a similar way, our “row” dynamics lead to discrete time $q$-PushTASEPs - new integrable particle systems in the Kardar-Parisi-Zhang universality class. We employ these new one-dimensional discrete time systems to establish a Fredholm determinantal formula for the two-sided continuous time $q$-PushASEP conjectured by Corwin-Petrov (2013). (2) In a certain Poisson-type limit (from discrete to continuous time), our two-dimensional dynamics reduce to the $q$-randomized column and row Robinson-Schensted correspondences introduced by O'Connell-Pei (2012) and Borodin-Petrov (2013), respectively. (3) In a scaling limit as $q\to1$, two of our four dynamics on interlacing arrays turn into the geometric RSK correspondences associated with log-Gamma or strict-weak directed random polymers.

    A q-deformation of the Robinson-Schensted-Knuth algorithm
  26. Ivan Corwin, Leonid Petrov. Stochastic higher spin vertex models on the line (2015) • Communications in Mathematical Physics 343 (2016), no. 2, 651-700 • arXiv:1502.07374 [math.PR] • (PDF) • (see also erratum below)
    Abstract

    We introduce a four-parameter family of interacting particle systems on the line which can be diagonalized explicitly via a complete set of Bethe ansatz eigenfunctions, and which enjoy certain Markov dualities. Using this, for the systems started in step initial data we write down nested contour integral formulas for moments and Fredholm determinant formulas for Laplace-type transforms. Taking various choices or limits of parameters, this family degenerates to many of the known exactly solvable models in the Kardar-Parisi-Zhang universality class, as well as leads to many new examples of such models. In particular, ASEP, the stochastic six-vertex model, $q$-TASEP and various directed polymer models all arise in this manner. Our systems are constructed from stochastic versions of the R-matrix related to the six-vertex model. One of the key tools used here is the fusion of R-matrices and we provide a probabilistic proof of this procedure.

  27. Alexei Borodin, Ivan Corwin, Leonid Petrov, Tomohiro Sasamoto. Spectral theory for interacting particle systems solvable by coordinate Bethe ansatz (2014) • Communications in Mathematical Physics 339 (2015), no. 3, 1167-1245 • arXiv:1407.8534 [math-ph] • (PDF) • (see also erratum below)
    Abstract

    We develop spectral theory for the $q$-Hahn stochastic particle system introduced recently by Povolotsky. That is, we establish a Plancherel type isomorphism result which implies completeness and biorthogonality statements for the Bethe ansatz eigenfunctions of the system. Owing to a Markov duality with the $q$-Hahn TASEP (a discrete-time generalization of TASEP with particles’ jump distribution being the orthogonality weight for the classical $q$-Hahn orthogonal polynomials), we write down moment formulas which characterize the fixed time distribution of the $q$-Hahn TASEP with general initial data.

    The Bethe ansatz eigenfunctions of the $q$-Hahn system degenerate into eigenfunctions of other (not necessarily stochastic) interacting particle systems solvable by the coordinate Bethe ansatz. This includes the ASEP, the (asymmetric) six-vertex model, and the Heisenberg XXZ spin chain (all models are on the infinite lattice). In this way, each of the latter systems possesses a spectral theory, too. In particular, biorthogonality of the ASEP eigenfunctions which follows from the corresponding $q$-Hahn statement implies symmetrization identities of Tracy and Widom (for ASEP with either step or step Bernoulli initial configuration) as corollaries. Another degeneration takes the $q$-Hahn system to the $q$-Boson particle system (dual to $q$-TASEP) studied in detail in our previous paper (2013).

    Thus, at the spectral theory level we unify two discrete-space regularizations of the Kardar-Parisi-Zhang equation / stochastic heat equation, namely, $q$-TASEP and ASEP.

  28. Alexey Bufetov, Leonid Petrov. Law of Large Numbers for Infinite Random Matrices over a Finite Field (2014) • Selecta Mathematica 21 (2015), no. 4, 1271-1338 • arXiv:1402.1772 [math.PR]
    Abstract

    Asymptotic representation theory of general linear groups $GL(n,q)$ over a finite field leads to studying probability measures $\rho$ on the group $U$ of all infinite uni-uppertriangular matrices over $F_q$, with the condition that $\rho$ is invariant under conjugations by arbitrary infinite matrices. Such probability measures form an infinite-dimensional simplex, and the description of its extreme points (in other words, ergodic measures $\rho$) was conjectured by Kerov in connection with nonnegative specializations of Hall-Littlewood symmetric functions.

    Vershik and Kerov also conjectured the following Law of Large Numbers. Consider an $n\times n$ diagonal submatrix of the infinite random matrix drawn from an ergodic measure coming from the Kerov’s conjectural classification. The sizes of Jordan blocks of the submatrix can be interpreted as a (random) partition of $n$, or, equivalently, as a (random) Young diagram $\lambda(n)$ with $n$ boxes. Then, as $n$ goes to infinity, the rows and columns of $\lambda(n)$ have almost sure limiting frequencies corresponding to parameters of this ergodic measure.

    Our main result is the proof of this Law of Large Numbers. We achieve it by analyzing a new randomized Robinson-Schensted-Knuth (RSK) insertion algorithm which samples random Young diagrams $\lambda(n)$ coming from ergodic measures. The probability weights of these Young diagrams are expressed in terms of Hall-Littlewood symmetric functions. Our insertion algorithm is a modified and extended version of a recent construction by Borodin and the second author (arXiv:1305.5501). On the other hand, our randomized RSK insertion generalizes a version of the RSK insertion introduced by Vershik and Kerov (1986) in connection with asymptotic representation theory of symmetric groups (which is governed by nonnegative specializations of Schur symmetric functions).

  29. Alexei Borodin, Leonid Petrov. Integrable probability: From representation theory to Macdonald processes (2013) • Probability Surveys, 11 (2014), 1-58 • arXiv:1310.8007 [math-ph]
    Abstract

    These are lecture notes for a mini-course given at the Cornell Probability Summer School in July 2013. Topics include lozenge tilings of polygons and their representation theoretic interpretation, the $(q,t)$-deformation of those leading to the Macdonald processes, nearest neighbor dynamics on Macdonald processes, their limit to semi-discrete Brownian polymers, and large time asymptotic analysis of polymer’s partition function.

    Large scale and long time behavior of a jumping interacting particle system
  30. Alexei Borodin, Ivan Corwin, Leonid Petrov, Tomohiro Sasamoto. Spectral theory for the q-Boson particle system (2013) • Compositio Mathematica, 151 (2015), no. 1, 1-67 • arXiv:1308.3475 [math-ph]
    Abstract

    We develop spectral theory for the generator of the $q$-Boson (stochastic) particle system. Our central result is a Plancherel type isomorphism theorem for this system. This theorem has various implications. It proves the completeness of the Bethe ansatz for the $q$-Boson generator and consequently enables us to solve the Kolmogorov forward and backward equations for general initial data. Owing to a Markov duality with $q$-TASEP, this leads to moment formulas which characterize the fixed time distribution of $q$-TASEP started from general initial conditions. The theorem also implies the biorthogonality of the left and right eigenfunctions.

    We consider limits of our $q$-Boson results to a discrete delta Bose gas considered previously by van Diejen, as well as to another discrete delta Bose gas that describes the evolution of moments of the semi-discrete stochastic heat equation (or equivalently, the O’Connell-Yor semi-discrete directed polymer partition function). A further limit takes us to the delta Bose gas which arises in studying moments of the stochastic heat equation / Kardar-Parisi-Zhang equation.

  31. Ivan Corwin, Leonid Petrov. The q-PushASEP: A New Integrable Model for Traffic in 1+1 Dimension (2013) • Journal of Statistical Physics, 160 (2015), no. 4, 1005-1026 • arXiv:1308.3124 [math.PR]
    Abstract

    We introduce a new interacting (stochastic) particle system $q$-PushASEP which interpolates between the q-TASEP introduced by Borodin and Corwin (see arXiv:1111.4408, and also arXiv:1207.5035; arXiv:1305.2972; arXiv:1212.6716) and the $q$-PushTASEP introduced recently by Borodin and Petrov (arXiv:1305.5501). In the $q$-PushASEP, particles can jump to the left or to the right, and there is a certain partially asymmetric pushing mechanism present. This particle system has a nice interpretation as a model of traffic on a one-lane highway in which cars are able to accelerate or slow down.

    Using the quantum many body system approach, we explicitly compute the expectations of a large family of observables for this system in terms of nested contour integrals. We also discuss relevant Fredholm determinantal formulas for the distribution of the location of each particle, and connections of the model with a certain two-sided version of Macdonald processes and with the semi-discrete stochastic heat equation.

  32. Alexei Borodin, Leonid Petrov. Nearest neighbor Markov dynamics on Macdonald processes (2013) • Advances in Mathematics, 300 (2016), 71-155 • arXiv:1305.5501 [math.PR]
    Abstract

    Macdonald processes are certain probability measures on two-dimensional arrays of interlacing particles introduced by Borodin and Corwin (arXiv:1111.4408 [math.PR]). They are defined in terms of nonnegative specializations of the Macdonald symmetric functions and depend on two parameters $(q,t)$, where $0\le q, t < 1$. Our main result is a classification of continuous time, nearest neighbor Markov dynamics on the space of interlacing arrays that act nicely on Macdonald processes.

    The classification unites known examples of such dynamics and also yields many new ones. When $t = 0$, one dynamics leads to a new integrable interacting particle system on the one-dimensional lattice, which is a $q$-deformation of the PushTASEP (= long-range TASEP). When $q = t$, the Macdonald processes become the Schur processes of Okounkov and Reshetikhin (arXiv:math/0107056 [math.CO]). In this degeneration, we discover new Robinson–Schensted-type correspondences between words and pairs of Young tableaux that govern some of our dynamics.

  33. Leonid Petrov. The Boundary of the Gelfand-Tsetlin Graph: New Proof of Borodin-Olshanski's Formula, and its q-analogue (2012) • Moscow Mathematical Journal, 14 (2014) no. 1, 121-160 • arXiv:1208.3443 [math.CO]
    Abstract

    In the recent paper [arXiv:1109.1412], Borodin and Olshanski have presented a novel proof of the celebrated Edrei-Voiculescu theorem which describes the boundary of the Gelfand-Tsetlin graph as a region in an infinite-dimensional coordinate space. This graph encodes branching of irreducible characters of finite-dimensional unitary groups. Points of the boundary of the Gelfand-Tsetlin graph can be identified with finite indecomposable (= extreme) characters of the infinite-dimensional unitary group. An equivalent description identifies the boundary with the set of doubly infinite totally nonnegative sequences.

    A principal ingredient of Borodin-Olshanski’s proof is a new explicit determinantal formula for the number of semi-standard Young tableaux of a given skew shape (or of Gelfand-Tsetlin schemes of trapezoidal shape). We present a simpler and more direct derivation of that formula using the Cauchy-Binet summation involving the inverse Vandermonde matrix. We also obtain a q-generalization of that formula, namely, a new explicit determinantal formula for arbitrary q-specializations of skew Schur polynomials. Its particular case is related to the q-Gelfand-Tsetlin graph and q-Toeplitz matrices introduced and studied by Gorin [arXiv:1011.1769].

  34. Leonid Petrov. Asymptotics of uniformly random lozenge tilings of polygons. Gaussian free field (2012) • Annals of Probability, 43 (2014), no. 1, 1-43 • arXiv:1206.5123 [math.PR]
    Abstract

    We study large-scale height fluctuations of random stepped surfaces corresponding to uniformly random lozenge tilings of polygons on the triangular lattice. For a class of polygons (which allows arbitrarily large number of sides), we show that these fluctuations are asymptotically governed by a Gaussian free (massless) field. This complements the similar result obtained in Kenyon [Comm. Math. Phys. 281 (2008) 675-709] about tilings of regions without frozen facets of the limit shape. In our asymptotic analysis we use the explicit double contour integral formula for the determinantal correlation kernel of the model obtained previously in arXiv:1202.3901 [math.PR].

  35. Leonid Petrov. Asymptotics of Random Lozenge Tilings via Gelfand-Tsetlin Schemes (2012) • Probability Theory and Related Fields, 160 (2014), no. 3, 429-487 • arXiv:1202.3901 [math.PR]
    Abstract

    A Gelfand-Tsetlin scheme of depth $N$ is a triangular array with m integers at level $m$, $m=1,\ldots,N$, subject to certain interlacing constraints. We study the ensemble of uniformly random Gelfand-Tsetlin schemes with arbitrary fixed $N$-th row. We obtain an explicit double contour integral expression for the determinantal correlation kernel of this ensemble (and also of its q-deformation).

    This provides new tools for asymptotic analysis of uniformly random lozenge tilings of polygons on the triangular lattice; or, equivalently, of random stepped surfaces. We work with a class of polygons which allows arbitrarily large number of sides. We show that the local limit behavior of random tilings (as all dimensions of the polygon grow) is directed by ergodic translation invariant Gibbs measures. The slopes of these measures coincide with the ones of tangent planes to the corresponding limit shapes described by Kenyon and Okounkov in arXiv:math-ph/0507007.

    We also prove that at the edge of the limit shape, the asymptotic behavior of random tilings is given by the Airy process.
    In particular, our results cover the most investigated case of random boxed plane partitions (when the polygon is a hexagon).

    A poem on the topic

    by OpenAI

    My sweet love's tiling, of lozenges arrayed,
    A pattern so beautiful and so fair,
    As if crafted by some celestial hand,
    Their beauty lies in the ordered array.

    The lozenges, red and blue, and green,
    Creating a pattern so pleasing to see,
    Their edges line up and fit so well,
    A tiling of lozenges, perfect and free.

    The asymptotic study of the tiling,
    Each lozenge in its place, and its fate,
    Is done through a Gelfand-Tsetlin scheme,
    And the resulting patterns so great.

    The lozenges in their ordered array,
    A pattern so pleasing and so fine,
    The study of their asymptotic fate,
    Will give us insight into the design.

    A frozen boundary curve inscribed in a polygon
  36. Leonid Petrov. sl(2) Operators and Markov Processes on Branching Graphs (2011) • Journal of Algebraic Combinatorics 38 (2013), no. 3, 663-720 • arXiv:1111.3399 [math.CO]
    Abstract

    We present a unified approach to various examples of Markov dynamics on partitions studied by Borodin, Olshanski, Fulman, and the author. Our technique generalizes the Kerov’s operators first appeared in [Okounkov, arXiv:math/0002135], and also stems from the study of duality of graded graphs in [Fomin, 1994].

    Our main object is a countable branching graph carrying an $\mathfrak{sl}(2,\mathbb{C})$-module of a special kind. Using this structure, we introduce distinguished probability measures on the floors of the graph, and define two related types of Markov dynamics associated with these measures. We study spectral properties of the dynamics, and our main result is the explicit description of eigenfunctions of the Markov generator of one of the processes.

    For the Young graph our approach reconstructs the z-measures on partitions and the associated dynamics studied by Borodin and Olshanski [arXiv:math-ph/0409075, arXiv:0706.1034]. The generator of the dynamics of [arXiv:math-ph/0409075] is diagonal in the basis of the Meixner symmetric functions introduced recently by Olshanski [arXiv:1009.2037, arXiv:1103.5848]. We give new proofs to some of the results of these two papers. Other graphs to which our technique is applicable include the Pascal triangle, the Kingman graph (with the two-parameter Poisson-Dirichlet measures), the Schur graph and the general Young graph with Jack edge multiplicities.

  37. Leonid Petrov. On Measures on Partitions Arising in Harmonic Analysis for Linear and Projective Characters of the Infinite Symmetric Group (2011) • Proceedings of the international conference "50 years of IITP" • arXiv:1107.0676 [math.CO]
    Abstract

    The z-measures on partitions originated from the problem of harmonic analysis of linear representations of the infinite symmetric group in the works of Kerov, Olshanski and Vershik (1993, 2004). A similar family corresponding to projective representations was introduced by Borodin (1997). The latter measures live on strict partitions (i.e., partitions with distinct parts), and the z-measures are supported by all partitions. In this note we describe some combinatorial relations between these two families of measures using the well-known doubling of shifted Young diagrams.

  38. Leonid Petrov. Pfaffian Stochastic Dynamics of Strict Partitions (2010) • Electronic Journal of Probability 16 (2011), 2246-2295 • arXiv:1011.3329 [math.PR]
    Abstract

    We study a family of continuous time Markov jump processes on strict partitions (partitions with distinct parts) preserving the distributions introduced by Borodin (1997) in connection with projective representations of the infinite symmetric group. The one-dimensional distributions of the processes (i.e., the Borodin’s measures) have determinantal structure. We express the dynamical correlation functions of the processes in terms of certain Pfaffians and give explicit formulas for both the static and dynamical correlation kernels using the Gauss hypergeometric function. Moreover, we are able to express our correlation kernels (both static and dynamical) through those of the z-measures on partitions obtained previously by Borodin and Olshanski in a series of papers. The results about the fixed time case were announced in the author’s note arXiv:1002.2714. A part of the present paper contains proofs of those results.

  39. Leonid Petrov. Random Strict Partitions and Determinantal Point Processes (2010) • Electronic Communications in Probability 15 (2010), 162-175 • arXiv:1002.2714 [math.PR]
    Abstract

    In this note we present new examples of determinantal point processes with infinitely many particles. The particles live on the half-lattice ${1,2,\ldots}$ or on the open half-line $(0,+\infty)$. The main result is the computation of the correlation kernels. They have integrable form and are expressed through the Euler gamma function (the lattice case) and the classical Whittaker functions (the continuous case). Our processes are obtained via a limit transition from a model of random strict partitions introduced by Borodin (1997) in connection with the problem of harmonic analysis for projective characters of the infinite symmetric group.

  40. Leonid Petrov. Random Walks on Strict Partitions (2009) • Journal of Mathematical Sciences 168 (2010), no. 3, 437-463 • arXiv:0904.1823 [math.PR]
    Abstract

    We consider a certain sequence of random walks. The state space of the n-th random walk is the set of all strict partitions of n (that is, partitions without equal parts). We prove that, as n goes to infinity, these random walks converge to a continuous-time Markov process. The state space of this process is the infinite-dimensional simplex consisting of all nonincreasing infinite sequences of nonnegative numbers with sum less than or equal to one. The main result about the limit process is the expression of its the pre-generator as a formal second order differential operator in a polynomial algebra. Of separate interest is the generalization of Kerov interlacing coordinates to the case of shifted Young diagrams.

  41. Leonid Petrov. Limit Behavior of Certain Random Walks on Strict Partitions (2009) • Russian Mathematical Surveys 64 (2009), no. 6, 1139-1141 •
  42. Leonid Petrov. A Two-parameter Family of Infinite-dimensional Diffusions in the Kingman Simplex (2007) • Functional Analysis and Its Applications 43 (2009), no. 4, 279-296 • arXiv:0708.1930 [math.PR]
    Abstract

    The aim of the paper is to introduce a two-parameter family of infinite-dimensional diffusion processes $X(\alpha,\theta)$ related to Pitman’s two-parameter Poisson-Dirichlet distributions $PD(\alpha,\theta)$. The diffusions $X(\alpha,\theta)$ are obtained in a scaling limit transition from certain finite Markov chains on partitions of natural numbers. The state space of $X(\alpha,\theta)$ is an infinite-dimensional simplex called the Kingman simplex. In the special case when parameter $\alpha$ vanishes, our finite Markov chains are similar to Moran-type model in population genetics, and our diffusion processes reduce to the infinitely-many-neutral-alleles diffusion model studied by Ethier and Kurtz (1981).

    Our main results extend those of Ethier and Kurtz to the two-parameter case and are as follows: The Poisson-Dirichlet distribution $PD(\alpha,\theta)$ is a unique stationary distribution for the corresponding process $X(\alpha,\theta)$; the process is ergodic and reversible; the spectrum of its generator is explicitly described. The general two-parameter case seems to fall outside the setting of models of population genetics, and our approach differs in some aspects from that of Ethier and Kurtz. We also consider the case of degenerate series of parameters $\alpha$ and $\theta$ and conclude that the diffusions in finite-dimensional simplexes studied by Ethier and Kurtz (1981) arise as a special case of our two-parameter family of diffusions.

    A dynamics of the four most common alleles. The hitting of finite-dimensional subspaces is evident
  43. Leonid Petrov. Asymptotic Behavior of a Certain Collection of Particles on a Line Under Synchronization (2006) • Proceedings of the XXVIII Conference of Young Scientists of Department of Mechanics and Mathematics of the Lomonosov Moscow State University (2006), 152-156, in Russian • • (PDF)

Errata

  1. Ivan Corwin, Leonid Petrov. Correction to "Stochastic higher spin vertex models on the line" (2019) • Commun. Math. Phys. 371, 353–355 (2019) • (PDF)
  2. Alexei Borodin, Ivan Corwin, Leonid Petrov, Tomohiro Sasamoto. Correction to "Spectral theory for interacting particle systems solvable by coordinate Bethe ansatz" (2019) • Commun. Math. Phys. 370, 1069–1072 (2019) • (PDF)

Other works

  1. Sihan Li, Andrew Mecca, Jeewoo Kim, Giusy Caprara, Elizabeth Wagner, Ting-Ting Du, Leonid Petrov, Wenhao Xu, Runjia Cui, Ivan Rebustini, Bechara Kachar, Anthony Peng, and Jung-Bum Shin, Myosin-VIIa is expressed in multiple isoforms and essential for tensioning the hair cell mechanotransduction complex. Nature Communications, 11, Article number: 2066 (2020). 15 pages.

Unpublished lecture notes

  1. Asymptotic Representation Theory, graduate topics course at University of Virginia, Fall 2022 • Course webpage with lecture notes • (PDF, 102 MB)
  2. Particle systems, graduate topics course at University of Virginia, Spring 2021 • Lecture notes in Obsidian format on github • (PDF, 312 MB)
  3. Random matrices, graduate topics course at University of Virginia, Fall 2019 • Course webpage with lecture notes • (PDF, 38 MB)
  4. Random matrices, graduate topics course at University of Virginia, Spring 2016 • Lecture notes on github • (PDF, 700 KB)
  5. Topics in Probability, graduate topics course at Northeastern University, Fall 2012 • Lecture notes at AMS Open Notes • (PDF, 1.7 MB)
  6. Course notes "Asymptotic representation theory", taught by G. Olshanski at the Independent University of Moscow, Fall 2009 and Spring 2010 (in Russian) • Webpage with notes • (PDF, 2.6 MB)

Slides of some talks

  1. How we can use AI in Math work (2024) • PDF (10.9 MB)
    Description

    These are the slides for the talk I gave at the University of Virginia on October 10, 2024 about how we can use AI in Math work.

  2. Grothendieck Shenanigans (2024) • PDF (7.2 MB)
    Description

    The story started with a problem of Stanley from his 2017 paper “Some Schubert shenanigans”: what is the asymptotically maximal value of a principal specialization of a Schubert polynomial S_w, and what does the corresponding permutation w look like? While this question is still out of reach, we investigate its variant for nonsymmetric Grothendieck polynomials. We analyze the asymptotic behavior of random permutations whose probabilities are proportional to the Grothendieck polynomials using TASEP and tools from integrable probability. The typical behavior of these permutations is described by a specific permuton (a continuous analog of a permutation). We also examine a family of atypical layered permutations that achieve the same asymptotically maximal weight.

    Based on the joint work with A.H. Morales, G. Panova, and D. Yeliussizov.

    A random pipe dream and its coloring leading to the Grothendieck random permutation
  3. Colored Particle Systems on the Ring: Stationarity from Yang-Baxter equation (2023) • PDF (8.9 MB)
    Description

    Recently, there has been much progress in understanding stationary measures for colored (also called multi-species or multi-type) interacting particle systems motivated by asymptotic phenomena and rich underlying algebraic and combinatorial structures (such as nonsymmetric Macdonald polynomials). I will describe a unified approach to constructing stationary measures for colored ASEP, q-Boson, and q-PushTASEP systems based on integrable stochastic vertex models and the Yang-Baxter equation. Stationary measures become partition functions of new “queue vertex models” on the cylinder, and stationarity is a direct consequence of the Yang-Baxter equation. Our construction recovers and generalizes known stationary measures constructed using multiline queues and the Matrix Product Ansatz. In the quadrant, Yang-Baxter implies a colored version of Burke’s theorem, which produces stationary measures for particle systems on the line. We also compute the colored particle currents in stationarity. Joint work with Amol Aggarwal and Matthew Nicoletti.

    Based on the joint work with Amol Aggarwal and Matthew Nicoletti.

    Colored Burke theorem in the quarter plane as a consequence of the Yang-Baxter equation
  4. Rewriting History in Integrable Stochastic Particle Systems (2023) • PDF (5.9 MB)
    Description

    Imagine two cars, slow (S) and fast (F), driving to the right on a discrete 1-dimensional lattice according to some random walk mechanism, and such that the cars cannot pass each other. We consider two systems, SF and FS, depending on which car is ahead. It is known for some time (through connections to symmetric functions and the RSK correspondence) that if at time 0 the cars are immediate neighbors, the trajectory of the car that is behind is the same (in distribution) in both systems. However, this fact fails when the initial locations of the cars are not immediate neighbors. I will explain how to recover the identity in distribution by suitably randomizing the initial condition in one of the systems.

    This result arises in our recent work on multiparameter stochastic systems (where the parameters are speeds attached to each car) in which the presence of parameters preserves the quantum integrability. This includes TASEP (totally asymmetric simple exclusion process), its deformations, and stochastic vertex models, which are all integrable through the Yang-Baxter equation (YBE). In the context of car dynamics, we interpret YBEs as Markov operators intertwining the transition semigroups of the dynamics of the processes differing by a parameter swap. We also construct Markov processes on trajectories which “rewrite the history” of the car dynamics, that is, produce an explicit monotone coupling between the trajectories of the systems differing by a parameter swap.

    Based on the joint work with Axel Saenz.

    Trajectories of two cars with different speeds and initial positions
  5. Inhomogeneous Interacting Particle Systems (2021) • PDF (6.7 MB)
    Description

    I will survey results on stochastic interacting particle systems (such as TASEP, the Totally Asymmetric Simple Exclusion Process) in the presence of inhomogeneity. That is, we consider particles with variable speeds, or the space in which the system evolves contains “swamps and highways”, where particles move with variable speed. Inhomogeneity inserts multiple parameters into the system, but in some miraculous cases the system stays exactly solvable in their presence. This allows to observe interesting asymptotic phase transitions. Moreover, permutations of the multiple parameters can sometimes be realized as Markov operators on the state of the system, leading to intriguing structural properties.

    The talk at the MSRI website

    Link to video at Vimeo

    Yang-Baxter equation for a vertex model
  6. Schur rational functions, vertex models, and random tilings (2021) • PDF (8.9 MB)
    Description

    Discusses symmetric functions and stochastic models based on the free fermionic six vertex model. Follows joint work with Aggarwal, Borodin, and Wheeler.

    The work deals with symmetric rational functions and probabilistic models based on the fully inhomogeneous six vertex (ice type) model satisfying the free fermion condition. Two families of symmetric rational functions $F_\lambda,G_\lambda$ are defined as certain partition functions of the six vertex model, with variables corresponding to row rapidities, and the labeling signatures $\lambda=(\lambda_1\ge \ldots\ge \lambda_N)\in \mathbb{Z}^N$ encoding boundary conditions. These symmetric functions generalize Schur symmetric polynomials, as well as some of their variations, such as factorial and supersymmetric Schur polynomials. Cauchy type summation identities for $F_\lambda,G_\lambda$ and their skew counterparts follow from the Yang–Baxter equation. Using algebraic Bethe Ansatz, we obtain a double alternant type formula for $F_\lambda$ and a Sergeev–Pragacz type formula for $G_\lambda$.

    In the spirit of the theory of Schur processes, we define probability measures on sequences of signatures with probability weights proportional to products of our symmetric functions. We show that these measures can be viewed as determinantal point processes, and we express their correlation kernels in a double contour integral form. We present two proofs: The first is a direct computation of Eynard–Mehta type, and the second uses non-standard, inhomogeneous versions of fermionic operators in a Fock space coming from the algebraic Bethe Ansatz for the six vertex model.

    We also interpret our determinantal processes as random domino tilings of a half-strip with inhomogeneous domino weights. In the bulk, we show that the lattice asymptotic behavior of such domino tilings is described by a new determinantal point process on $\mathbb{Z}^{2}$, which can be viewed as an doubly-inhomogeneous generalization of the extended discrete sine process.

    Inhomogeneous two-dimensional discrete sine kernel
  7. Random polymers and symmetric functions (2020) • PDF (12.2 MB)
    Description

    Surveys integrable random polymers (based on gamma / inverse gamma or beta distributed weights), and explains their connection to symmetric functions. Based on a joint work with Matteo Mucciconi.

    Conjectural orthogonality for N=2
  8. Spin deformation of q-Whittaker polynomials and Whittaker functions (2020) • PDF (33.6 MB)
    Description

    Spin $q$-Whittaker symmetric polynomials labeled by partitions $\lambda$ were recently introduced by Borodin and Wheeler (arXiv:1701.06292) in the context of integrable $\mathfrak{sl}_2$ vertex models. They are a one-parameter deformation of the $t=0$ Macdonald polynomials. We present a new, more convenient modification of spin $q$-Whittaker polynomials and find two Macdonald type $q$-difference operators acting diagonally in these polynomials with eigenvalues, respectively, $q^{-\lambda_1}$ and $q^{\lambda_N}$ (where $\lambda$ is the polynomial’s label). We study probability measures on interlacing arrays based on spin $q$-Whittaker polynomials, and match their observables with known stochastic particle systems such as the $q$-Hahn TASEP.

    In a scaling limit as $q\nearrow 1$, spin $q$-Whittaker polynomials turn into a new one-parameter deformation of the $\mathfrak{gl}_n$ Whittaker functions. The rescaled Pieri type rule gives rise to a one-parameter deformation of the quantum Toda Hamiltonian. The deformed Hamiltonian acts diagonally on our new spin Whittaker functions. On the stochastic side, as $q\nearrow 1$ we discover a multilevel extension of the beta polymer model of Barraquand and Corwin (arXiv:1503.04117), and relate it to spin Whittaker functions.

    Based on a joint work with Matteo Mucciconi and earlier works with Alexey Bufetov and both of them.

    An example of the Yang-Baxter equation in the Schur case
  9. Mapping TASEP back in time (2019) • PDF (13.5 MB)
    Description

    We obtain a new relation between the distributions $\mu_t$ at different times $t ≥ 0$ of the continuous-time TASEP (Totally Asymmetric Simple Exclusion Process) started from the step initial configuration. Namely, we present a continuous-time Markov process with local interactions and particle-dependent rates which maps the TASEP distributions μt backwards in time. Under the backwards process, particles jump to the left, and the dynamics can be viewed as a version of the discrete-space Hammersley process. Combined with the forward TASEP evolution, this leads to a stationary Markov dynamics preserving $\mu_t$ which in turn brings new identities for expectations with respect to $\mu_t$. Based on a joint work with Axel Saenz.

    Note that the original keynote presentation contained videos which are not included in the PDF download.

    A sample of the stationary dynamics on TASEP distribution
  10. From infinite random matrices over finite fields to square ice (2019) • PDF (32 MB)
    Description

    Asymptotic representation theory of symmetric groups is a rich and beautiful subject with deep connections with probability, mathematical physics, and algebraic combinatorics. A one-parameter deformation of this theory related to infinite random matrices over a finite field leads to a randomization of the classical Robinson-Schensted correspondence between words and Young tableaux. Exploring such randomizations we find unexpected applications to six vertex (square ice) type models and traffic systems on a 1-dimensional lattice.

    A simulation of the square ice, due to Shreyas Balaji (MIT UROP)
  11. Gibbs measures, arctic curves, and random interfaces (2018) • PDF (35 MB)
    Description

    This talk outlines connections between 2-dimensional Gibbs measures with a height function and particle systems in the Kardar-Parisi-Zhang universality class.

    An illustration of the Gibbs property
  12. Nonequilibrium particle systems in inhomogeneous space (2018) • PDF (5 MB)
    Description

    This talk describes results on continuous space TASEP in inhomogeneous space, based on papers with Borodin and with with Knizel and Saenz, and on some work in progress.

  13. Spectral theory for interacting particle systems (2014) • PDF (1 MB)
    Description

    This talk describes results on spectral theory for q-Hahn zero-range process, ASEP, six-vertex model, and q-TASEP. Based on [14] and [17].

  14. Integrable Probability: Random Polymers, Random Tilings, and Interacting Particle Systems (2013) • PDF (6 MB)
    Description

    One of the versions of my “job talk” in Fall 2013 describing many facets of integrable probability. It is supposed to be accessible. The talk is based on [15] and on the previous two talks. More details can also be found in arXiv:1106.1596 [math.PR] by Corwin and arXiv:1212.3351 [math.PR] by Borodin and Gorin.

    O'Connell-Yor directed random polymer
  15. Markov Dynamics on Interlacing Arrays (2013) • PDF (7 MB)
    Description

    The talk is devoted to the construction of Markov dynamics on interlacing arrays which act nicely on the Macdonald measures. In a particular case one gets $q$-deformed Robinson-Schensted insertion algorithms. The talk is based on [12], [13], see also [14], [15].

  16. Random 3D surfaces and their asymptotic behavior (2012) • PDF (6 MB)
    Description

    The talk describes the results of [9], [10], and [11] on asymptotic behavior of random lozenge tilings via determinantal structure and double contour integral formulas for the correlation kernel.

  17. Operators and Markov Dynamics on Branching Graphs (2011) • PDF (1.5 MB)
    Description

    The talk is based on [8] and describes $\mathfrak{sl}(2,\mathbb{C})$ structures behind Markov jump processes on the Young and related branching graphs

  18. Infinite-dimensional Diffusions Related to the Two-parameter Poisson-Dirichlet Distributions (2010) • PDF (1 MB)
    Description

    The talk describes population genetics perspective behind infinite-dimensional diffusions preserving the two-parameter Poisson–Dirichlet distributions and related models. It is based on [2].

  19. Infinite-Dimensional Diffusion Processes Approximated by Finite Markov Chains on Partitions (2009) • PDF (2 MB)
    Description

    The talk describes algebraic/combinatorial perspective behind infinite-dimensional diffusions preserving the two-parameter Poisson–Dirichlet distributions and related models. It is based on [2], see also [4], [8]

Preprints Publications Errata Lecture notes Slides Gallery

Google scholar Research travel

BiBTeX file

NSF FRG page