Blue Ridge Probability Day

EGMT 1520 • Building Truth from Scratch (Empirical & Scientific Engagement)
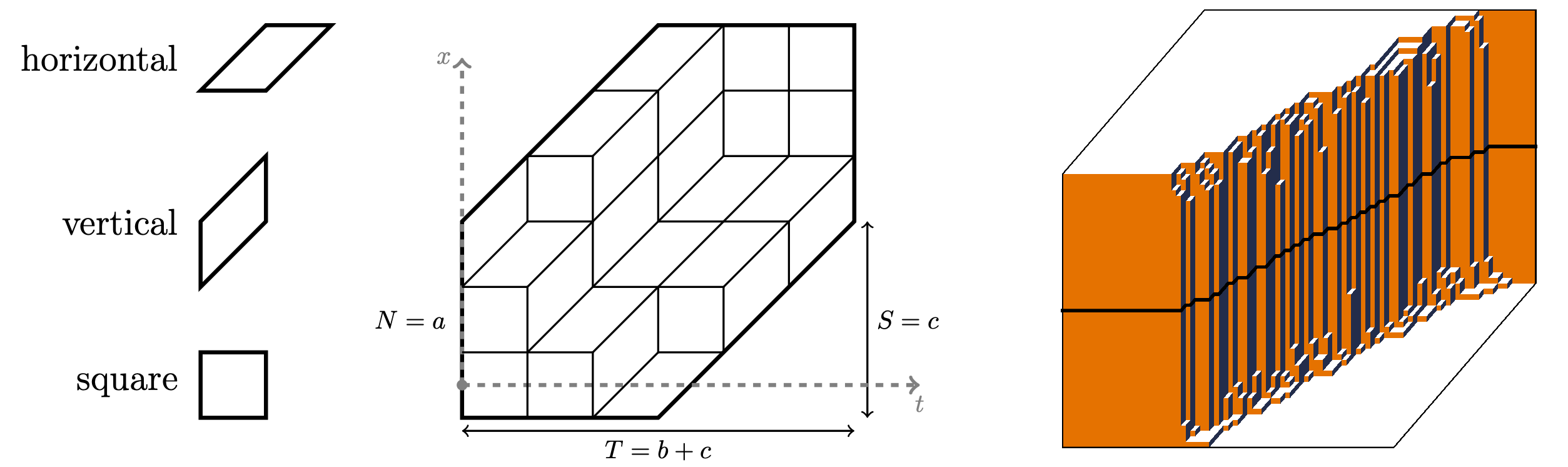
Random Lozenge Waterfall: Dimensional Collapse of Gibbs Measures
We investigate the asymptotic behavior of the $q$-Racah probability measure on lozenge tilings of a hexagon whose side lengths scale linearly with a parameter $L\to\infty$, while the parameters $q\in(0,1)$ and $\kappa\in \mathbf{i}\mathbb{R}$ remain fixed. This regime differs fundamentally from the traditional case $q\sim e^{-c/L}\to1$, in which random tilings are locally governed by two-dimensional translation-invariant ergodic Gibbs measures. In the fixed-$q$ regime we uncover a new macroscopic phase, the waterfall (previously only observed experimentally), where the two-dimensional Gibbs structure collapses into a one-dimensional random stepped interface that we call a barcode.
We prove a law of large numbers and exponential concentration, showing that the random tilings converge to a deterministic waterfall profile. We further conjecture an explicit correlation kernel of the one-dimensional barcode process arising in the limit. Remarkably, the limit is invariant under shifts by $2\mathbb{Z}$ but not by $\mathbb{Z}$, exhibiting an emergent period-two structure absent from the original weights. Our conjectures are supported by extensive numerical evidence and perfect sampling simulations. The kernel is built from a family of functions orthogonal in both spaces $\ell^{2}(\mathbb{Z})$ and $\ell^{2}(\mathbb{Z}+\frac12)$, that may be of independent interest.
Our proofs adapt the spectral projection method of Borodin–Gorin–Rains (2009) to the regime with fixed $q$. The resulting asymptotic analysis is substantially more involved, and leads to non-self-adjoint operators. We overcome these challenges in the exponential concentration result by a separate argument based on sharp bounds for the ratios of probabilities under the $q$-Racah orthogonal polynomial ensemble.
Bibliography sorting tool for LaTeX alpha style and amsrefs
![A random domino tiling of the Aztec diamond of size 300 with i.i.d. continuous uniform random weights on [0,2] A random domino tiling of the Aztec diamond of size 300 with i.i.d. continuous uniform random weights on [0,2]](https://storage.lpetrov.cc/img/papers/300_uniform.jpg)
Domino Tilings of the Aztec Diamond in Random Environment and Schur Generating Functions
We study the asymptotic behavior of random domino tilings of the Aztec diamond of size $M$ in a random environment, where the environment is a one-periodic sequence of i.i.d. random weights attached to domino positions (i.e., to the edges of the underlying portion of the square grid). We consider two cases: either the variance of the weights decreases at a critical scale $1/M$, or the distribution of the weights is fixed. In the former case, the unrescaled fluctuations of the domino height function are governed by the sum of a Gaussian Free Field and an independent Brownian motion. In the latter case, we establish fluctuations on the much larger scale $\sqrt M$, given by the Brownian motion alone.
To access asymptotic fluctuations in random environment, we employ the method of Schur generating functions. Moreover, we substantially extend the known Law of Large Numbers and Central Limit Theorems for particle systems via Schur generating functions in order to apply them to our setting. These results might be of independent interest.
Teaching with AI: Reflections and Practical Examples
Presentation on integrating AI tools into the teaching workflow, covering practical examples, live demonstrations, and reflections on the changing landscape of education with AI assistance. Topics include using AI for problem generation, student interaction patterns, and maintaining academic integrity while leveraging these powerful tools.
The presentation includes hands-on examples with Claude, demonstrations of real-time problem-solving, and discussion of pedagogical implications. Special attention is given to the balance between AI assistance and developing students’ independent thinking skills.
Note: These slides were created using Marp and are best viewed in a modern web browser. Use arrow keys or spacebar to navigate.