Colored Interacting Particle Systems on the Ring: Stationary Measures from Yang--Baxter Equation
2023/09/13
Amol Aggarwal, Matthew Nicoletti, Leonid PetrovCompositio Math., to appear • arXiv:2309.11865 [math.PR]
Source
Recently, there has been much progress in understanding stationary measures for colored (also called multi-species or multi-type) interacting particle systems, motivated by asymptotic phenomena and rich underlying algebraic and combinatorial structures (such as nonsymmetric Macdonald polynomials).
In this paper, we present a unified approach to constructing stationary measures for most of the known colored particle systems on the ring and the line, including (1) the Asymmetric Simple Exclusion Process (multispecies ASEP, or mASEP); (2) the q-deformed Totally Asymmetric Zero Range Process (TAZRP) also known as the q-Boson particle system; (3) the q-deformed Pushing Totally Asymmetric Simple Exclusion Process (q-PushTASEP). Our method is based on integrable stochastic vertex models and the Yang-Baxter equation. We express the stationary measures as partition functions of new “queue vertex models” on the cylinder. The stationarity property is a direct consequence of the Yang-Baxter equation.
For the mASEP on the ring, a particular case of our vertex model is equivalent to the multiline queues of Martin. For the colored q-Boson process and the q-PushTASEP on the ring, we recover and generalize known stationary measures constructed using multiline queues or other methods by Ayyer-Mandelshtam-Martin (1, 2, and Bukh-Cox. Our proofs of stationarity use the Yang-Baxter equation and bypass the Matrix Product Ansatz (used for the mASEP by Prolhac-Evans-Mallick).
On the line and in a quadrant, we use the Yang-Baxter equation to establish a general colored Burke’s theorem, which implies that suitable specializations of our queue vertex models produce stationary measures for particle systems on the line. We also compute the colored particle currents in stationarity.
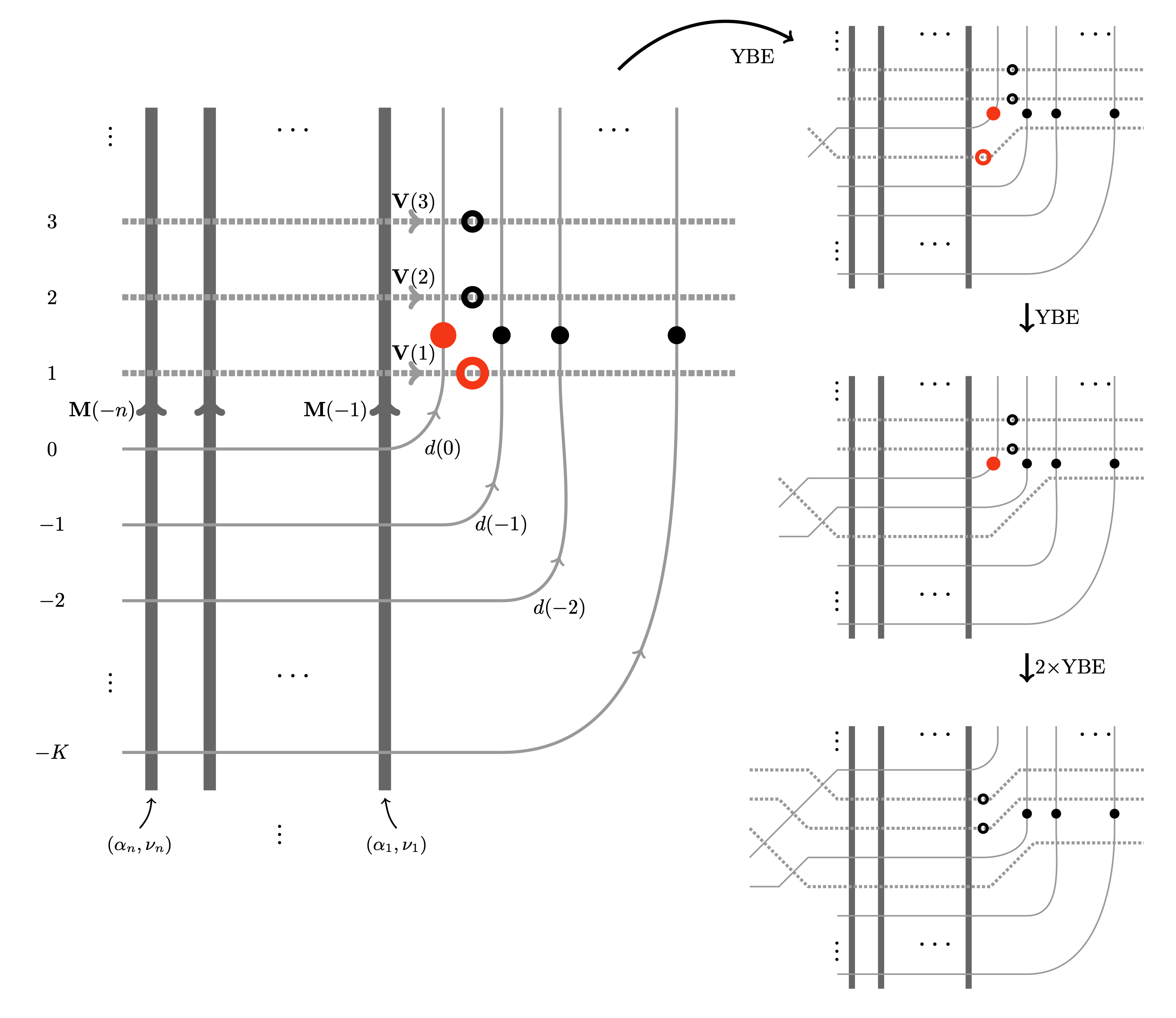
Yang-Baxter equation implies colored Burke theorem