(Old) Gallery of simulations

Simulations of inhomogeneous multilayer pushTASEP
I’ve done some simulations of a multilayer version of the pushTASEP in inhomogeneous space, in my new simulations gallery.
Technical details and more pictures are here.
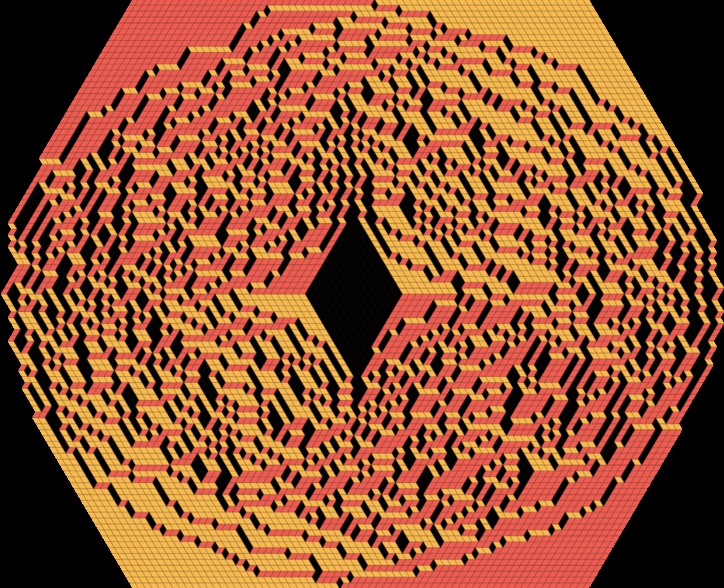
Pictures and movies of random lozenge tilings
In Spring 2015 and Summer 2016 I used the Python and Mathematica as briefly described here to produce a number of pictures and “movies” of random lozenge tilings. Some of these pictures even appeared at an art exhibition at Harvard’s Radcliffe Institute accompanying Alexei Borodin’s fellowship.
These pictures and “movies” of random tilings are collected in this post.
Dear colleagues:
Feel free to use these pictures to illustrate your research in talks and papers, with attribution (CC BY-SA 4.0). Some of the images are available in very high resolution upon request.

Simulations of stochastic higher spin vertex model
The stochastic higher spin vertex model introduced in my paper with Ivan Corwin ([arXiv:1502.07374 [math.PR]][ivan6v]) generalizes the stochastic six vertex model considered by Borodin, Corwin, and Gorin, arXiv:1407.6729 [math.PR]. Here are some simulations related to this model.
Dear colleagues:
Feel free to use these pictures to illustrate your research in talks and papers, with attribution (CC BY-SA 4.0). Some of the images are available in very high resolution upon request.

Implementation of Glauber dynamics simulation of random lozenge tilings
I’ve implemented the Glauber dynamics to (approximately) sample uniformly random lozenge tilings of polygons of Gelfand-Tsetlin type. These polygons are called sawtooth domains by J. Novak. This paper by B. Laslier and F.L. Toninelli establishes rate of convergence of the Glauber dynamics to the uniformly random lozenge tiling.